I’ve seen lots of hocus-pocus out there on where the UARS spacecraft re-entered. Lots of bogus videos are out along with vague descriptions of where the spacecraft landed (some that narrow it down to the Pacific Ocean). While NASA’s taking their time giving us an impact point, they are giving us enough information to calculate one ourselves. Thus, I will take the liberty of doing so. I’ll say a few things about it and then take a wild flying guess (WFG) at where it hit in the ocean based on the few pieces of information we do have.
First off, the reentry of spacecraft is not an exact science. The atmospheric density, especially at the high altitudes where spacecraft fly, is hard to predict. Solar activity (and there’s been a lot of that lately) can increase the extent of the atmosphere and this is difficult to model in real time. In addition, when a spacecraft is tumbling (as numerous videos shot by amateur astronomers on the ground showed UARS was doing) it becomes difficult to estimate the surface area that the atmosphere encounters as the spacecraft plows through it (critical for prediction). Imagine sticking your hand out the window of your car while driving. Palm into the wind, you feel more resistance. Edge-on to the wind, you feel less. UARS is tumbling, so the resistance (or drag) isn’t constant. The Aerospace corporation has a nice write-up on re-entry here: Spacecraft Reentry
I have some pretty good software at my disposal (Satellite Tool Kit, from Analytical Grapics Inc. and I’ll use that to make my guess for me.
My WFG will be based on a few things I know:
1. The latest set of Two Line Elements (TLE). These orbital elements come from AGI, which got them from TS Kelso, who got them from where he normally does on Celestrak . Last set is from Sep. 24 at about 2:37 UTC.
2. NASA is saying that the spacecraft “reentered” at 4:16 UTC on Sept. 24. I’m going to assume reentry means that it reached 75 km in altitude. The spacecraft will be breaking up at that point, but I’ll model it all the way to the ground as if it didn’t. That should give us a good guess at the maximum distance any piece will travel.
3. Spacecraft Mass of 5668 kg (12,495 lb) and dimensions of 15 ft wide x 35 ft. long which gives a surface area of about 525 sq ft (48.7 sq m) . These should be fairly close. UARS gives us the dry mass (fuel is mostly gone) and the projected area comes from Space.com
4. Coefficient of drag. (Cd) A default number (used in STK) for spacecraft is 2.2 (unitless) but I’m going to vary this.
To guess the re-entry time, I’m going to take my TLE I mentioned above, and use that to seed my high-precision numerical integrator (STK/Astrogator)
Now it’s time to get technical. The TLE will provide the initial orbit state, and I’ll use the values I give above for Mass and surface area. I’ll start off with a default Cd of 2.2. Then, I will integrate forward until my spacecraft reaches an altitude of 75 km (46 miles). I’m using a 21 x 21 gravity field (overkill for one orbit), Lunar and Solar perturbations (overkill), Solar Radiation Pressure (overkill) and the Jacchia-Roberts Atmospheric Density model. These are the default settings in STK/Astogator, and they are fine for this application. Then, I’m going to use the differential corrector in STK/Astrogator (a “shooting method” targeter) to vary my Cd in order to have me hit an altitude of 75 km at 04:15 UTC on Sept. 24, 2013. Why vary the Cd? I don’t know the exact surface area the atmosphere is encountering, and modeling that is next to impossible. We don’t know the atmosphere that well when it’s coming in either. When these things are used in the numerical integration they are multiplied together, so it’s ok to use Cd as a universal “fudge factor” and vary it to get what we want. If we were controlling the spacecraft, we could do much better. We’d be able to accurately predict the surface area and the Cd, and the only real variable after that would be the atmosphere. That’s still a big variable if there’s a lot of solar activity, but the message here is that uncontrolled reentry + tumbling + solar activity = unpredictable impact point.
Now all of this may sound dirt-simple to you (or not) but I guarantee that the folks at NASA and JSpOC are doing something very similar (if not identical). They may have better data than what they are giving me (TLEs are fairly low-precision) but their software isn’t any better than what I’m using. STK is being used to fly missions all over the solar system and in Earth orbit, and was used to reenter a commercial spacecraft earlier this year (more on that in an upcoming post). If you want to see another measure of the precision of this software, see my earlier post about the ISS near-miss back in August.
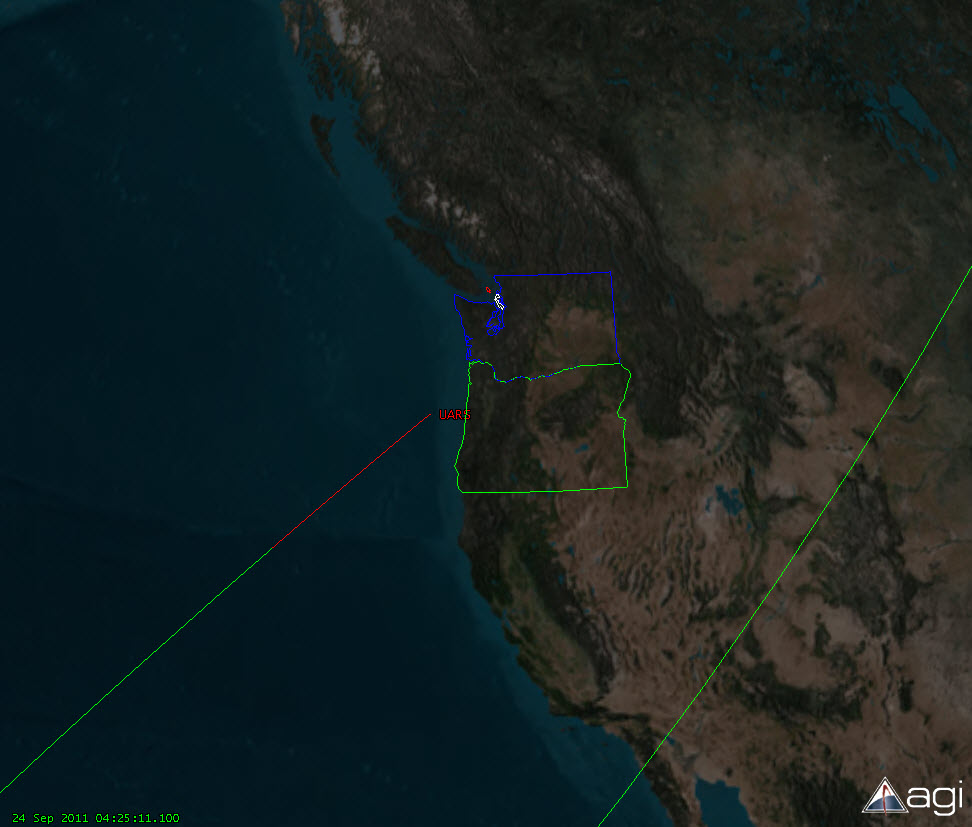
I varied Cd so that I hit 75 km in altitude at 4:15 UTC, and here’s what we get:
The green line is the orbit track (in an earth-fixed projection onto the surface). The eastern track over the US is the last track before reentry, the track coming from the lower left corner is the continuation of that track after a rev. The spot where the green track ends and the red track begins is the 75 km altitude mark at 4:16 UTC. The end of the red track (labeled “UARS”) is where the spacecraft would have impacted if it stayed completely intact (which it didn’t). The time you see in the lower left (4:25:11) is the time when UARS would have hit the ocean, if the spacecraft had stayed intact.
Where did the pieces land? My guess is an impact zone spread out probably 500 miles long before the end of the red line. Or, in other words, about the length of the red part of the orbit track on the ground (which is roughly 460 miles).
That little red island up north of Seattle and east of the southern tip of Vancouver Island is where I live, and me and 20 other friends of mine scattered all over western Washington saw nothing as we stood outside yesterday looking. That’s because the UARS cloud of stuff went for a swim before it got to us. Bugger.
My WFG says that UARS is in the ocean off the coast of Oregon and California. That’s why NASA is hinting (on their twitter feed for UARS) that some fishermen might have seen it.
UPDATE 6:30 PM PDT, 9/25/11
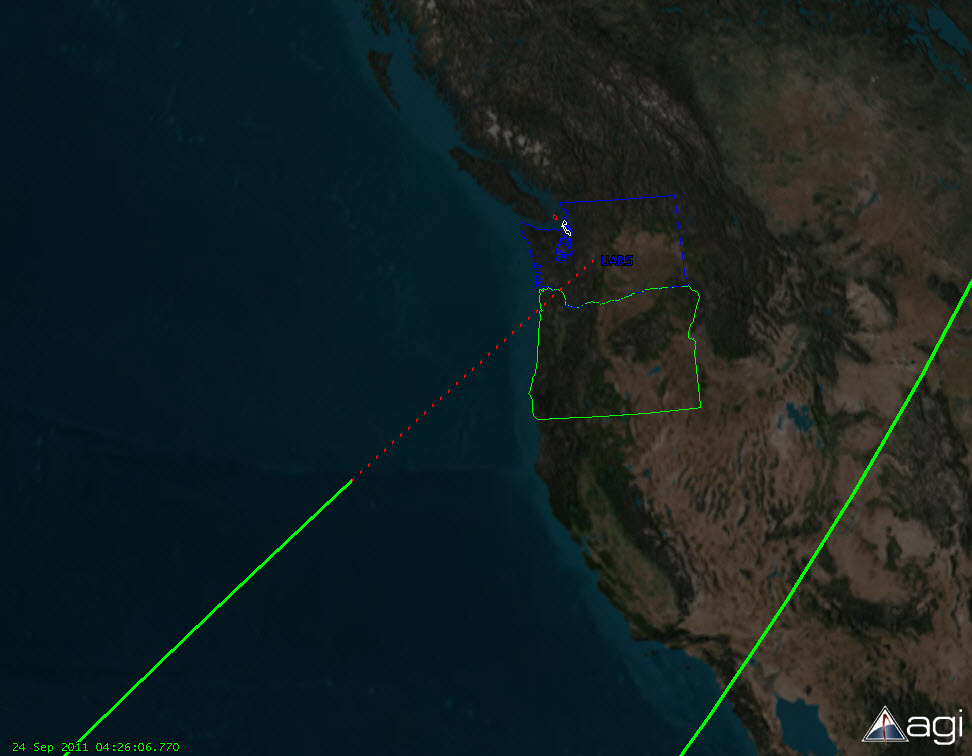
Our friends at @UARS_Reentry on Twitter are now tweeting the possibility of a piece of UARS reaching Washington State. Very small changes to my assumptions will allow this. Let’s go back and change the assumption in number 2 above that 75 km “defines” entry into the atmosphere. Let’s change that to 80 km. Let’s see if that makes a difference:
That almost allows pieces to hit Portland, but not quite Washington. Hmm. One other assumption we could look at is the time. 4:16 UTC is a pretty round number. That could be anything from 4:15:31 to 4:16:29. Since earlier times will back us further out into the water, we’ll go later. Let’s try an entry at 80 km at 4:16:29 UTC:
Looks possible to me.