Phasing Loops and the LADEE trajectory
Many people have asked about LADEE’s trajectory, which uses 3 and a half “phasing loops” to get to the Moon. On one of my other postings, a reader asked if phasing loops saved delta-v on the trans-lunar injection (TLI) burn. The answer is no. The cost (in delta-v) to get to a lunar transfer from a specific injection orbit (for example the 6.4 day orbit LADEE currently is in) is the same if you go direct as it is if you go around a few times first.
The savings come elsewhere, in particular with the cost of correcting for errors from the launch vehicle (rocket).
There are four important reasons why phasing loops are being used for LADEE.
1. Mass
The Minotaur V couldn’t throw the whole mass of LADEE all the way to Lunar Injection.
2. Launch Dispersions
Let me borrow from my answer in the comments section on a previous post:
The Minotaur V, which is a stack of 5 solids, isn’t considered to be a particularly precise rocket. In other words, if we were to ask for a 6.3 day orbit, we might get a 5 day orbit, or we might get an 8 day orbit. In a direct injection trajectory (such as the 3-day missions used by Apollo), injection errors can only be corrected out after good amount of tracking can be done (~ 24 hrs normally) to determine the orbit (OD, or “Orbit Determination”). However, as the spacecraft gets further and further away from the Earth, the cost of correcting out launch errors gets larger as well. Often times, by the time enough tracking data can be gathered, the cost of correcting out any launch errors can be 5-10 times the actual size of the error. So a 5 m/sec error would take 25 m/sec to correct, etc.
If, instead of using a direct approach, you use phasing loops the cost is a lot closer to 1:1 (i.e. a 5 m/sec error in launch costs 5 m/sec to correct, or can even save you fuel). It’s not a pure 1:1 ratio, because there is a timing aspect as well, but in terms of the energy of the orbits, it is 1:1.
Assume that you’re going to launch to a 6.4 day orbit and that you’ll then transfer to an 7.6 day orbit, and then a 10 day orbit, and then spend 5 days getting to the Moon (total of 29 days). The cost of transferring to the 5-day lunar transfer from the 6.4 day starting orbit is always the same. Now say that your rocket doesn’t give you exactly what you want, and instead of a 6.4 day orbit, you are inserted into a 7 day orbit. Instead of doing a TCM to correct out that error, you simply replan your trajectory profile. You spend 7 days in the first orbit, but instead of transferring to a 7.6 day orbit, your first maneuver is zero, and you stay in the 7 day orbit for 2 days. So your first rev is 7 days, second rev is 7 days, and then you transfer to a 10 day orbit, and take 5 more to get to the Moon (still 29).
Same thing if you are launched to a 5 day orbit. The second orbit can be 9 days, the third 10, and 5 days to the Moon (29 days total again).
You get the picture.
The total delta-v to get to the Moon doesn’t really change, but your orbit profile is flexible to large dispersions in your injection.
Phasing loops have been used on many other missions (Clementine and WMAP are 2 good examples). I designed the phasing loops on LADEE to accommodate the Minotaur V dispersions. The LADEE spacecraft barely had enough fuel to do its science mission, and the choice of phasing loops allowed the mission to accommodate the Minotaur V dispersions, at the cost of some extra time in cislunar space. The operations costs are not free (of course), but if you can’t fit on the rocket, sometimes you don’t have a mission.
[Funny thing is that although the Minotaur V is “supposed” to have large dispersions, the fact is that the launch last Friday (Sept 7, 2013) was just about perfect. We got almost precisely the nominal trajectory, in what probably is the most precise injection a Minotaur rocket has ever done. Had we known in advance that we could have gotten such an injection, we probably would have gone direct.]
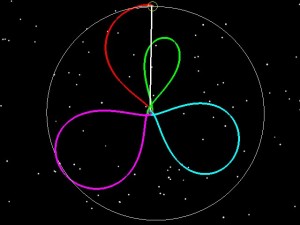
So here are a few examples of how phasing loops allow you flexibility. As stated previously, LADEE was launched into a 6.4 day orbit. However, let’s say LADEE got into a 5 Day orbit instead:
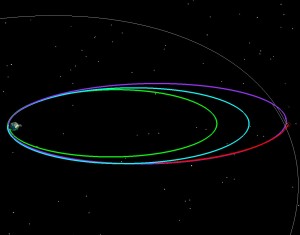
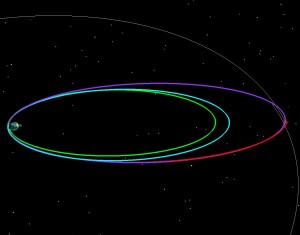
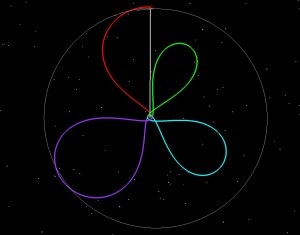
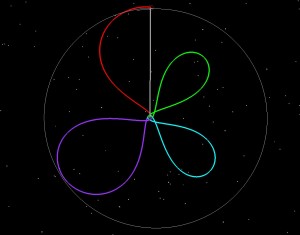
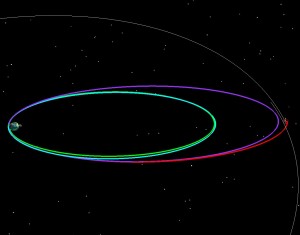
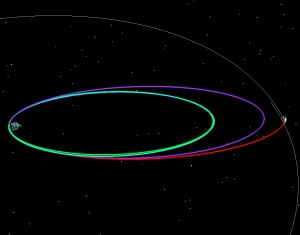
If LADEE had been launched into a 5 day orbit (green), we then could have raised the 2nd orbit to have a 9.5 day period (blue), and the third to have a 9.8 day period purple and then done our normal 5 day transfer to the Moon. The two pictures below tell the story. On the left the orbit is shown in an Earth-Moon Rotating coordinate system. The Earth is in the middle, and the Moon is stationary from the top. Imagine that you’re way above the Earth-Moon system, and that you are slowly rotating at exactly the same rate as the Moon goes around the Earth. On the right is the normal view, an Earth-centered inertial frame.
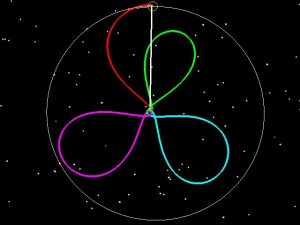
If LADEE had been launched into a 6 day orbit (green), we then could have raised the 2nd orbit to have an 8.3 day period (blue), and the third to have a 9.9 day period purple and then done our normal 5 day transfer to the Moon.
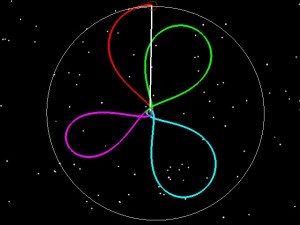
If LADEE had been launched into a 7 day orbit (green), we then could have raised the 2nd orbit to have an 8.1 day period (blue), and the third to have a 9 day period purple and then done our normal 5 day transfer to the Moon.
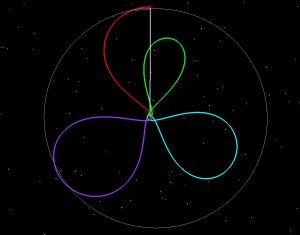
If LADEE had been launched into an 8 day orbit (green), we then could have raised the 2nd orbit to have an 8.4 day period (blue), lowered the third to have a 7.7 day period purple and then done our normal 5 day transfer to the Moon. The 8 day orbit and above starts to cost more energy, because you have to lower the 2nd orbit and then raise it back up for the third. So in this case, while the rocket would have placed us in a higher orbit than we wanted (and thus you’d think it might save us energy) we end up having to pay a bit extra to get the timing right.
Note here that all the examples I show have us keeping the time of the third perigee mostly constant, along with the time of flight between that perigee and the Moon constant at 5 days. This comes from the fact that once we’ve launched and the Minotaur Stage 5 has fired, our line of apsides (between apogee and perigee) is mostly fixed in space (actually it was fixed before launch for optimization purposes, but that’s another topic) and we are now locked into getting at the Moon when the Moon is at the same latitude as our apogee.
3. Widening the Launch Window
Another thing phasing loops give you are a wider launch window. With the argument of perigee (and thus the line of apsides) fixed before launch, we are fixed to arrive at the Moon when it as a specific latitude (same as our apogee). Given that, a direct launch would have only had a very short launch period if you assume that you’re always launching with the same energy from the upper stage. Phasing loops allow you to widen the window up to 5 days. In the case of LADEE, we actually launched on the first day of the launch period (on the first second of the launch window) but we were lucky. We’ll take the luck, but we didn’t plan for it. Instead, we had a 5 day window.
On the first day of the launch window (Sep. 6, 2013), our first orbit would be 6.4 days, the 2nd 7.95, the third 9.95 and then about 5 days to the Moon.
On the second day of the launch window (Sep. 7, 2013), our first orbit would be 6.33 days [Note: the rocket is always launching us to the same orbit, but the Moon’s gravity alters our orbit a bit, so the first rev doesn’t always have the same period] , the 2nd 7.00, the third 9.95 and then about 5 days to the Moon.
On the third day of the launch window (Sep. 8, 2013), our first orbit would be 6.24 days, the 2nd 6.32, the third 9.55 and then about 5 days to the Moon.
On the fourth day of the launch window (Sep. 9, 2013), our first orbit would be 6.19 days, the 2nd 6.27, the third 8.82 and then about 5 days to the Moon.
The last day of the launch window (Sep. 10, 2013), our first orbit would be 6.16 days, the 2nd 6.32, the third 7.95 and then about 5 days to the Moon.
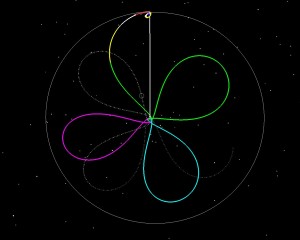
Why does the launch period stop? Look at the rotating frame picture in each of the examples. Think of the picture in terms of quadrants, with the first quadrant being in the upper right, second in the lower right, third in the lower left, and 4th in the upper left. Any loop in the first quadrant gets to apogee with the Moon in front of it. This is fine, because the gravity of the Moon will give us some extra velocity at apogee, and will raise our subsequent perigee altitude. The closer we are to the Earth-Moon line (the vertical white line in the rotating frame picture), the more boost we get from the Moon. The further away we are from the Moon, the less boost we get. Going into the 4th quadrant is bad, because if we get in front of the Moon at apogee, then the Moon’s gravity slows us down, and drives the perigee altitude into the Earth. In the 2nd quadrant we get slight gravitational lowering at perigee, and the 3rd we get slight gravitational raising. If you watch the sequence through the launch period, you see that each day the first loop clocks further (clockwise) to the right, closer to the 2nd quadrant. We have to launch to get our orbital plane to match the Moon’s on arrival, and also have to make this happen when the Moon has the same latitude as our apogee.
This is all important for the trajectory planning of LADEE, because when you launch off a rocket from the Earth, your insertion perigee is usually low (200 km). You don’t want to come back at this altitude the next time around. So we launch when the Moon will raise us (without requiring a maneuver at apogee, which we could also do, but we’d rather not require a maneuver at the first apogee to keep the spacecraft from hitting the Earth). So as long as our first loop stays within the first quadrant in the rotating frame, we’re OK. This gives us a 4-5 day launch window (some times we lose the first day if we decide that potential launch dispersions will throw too many statistical cases into the 4th quadrant.)
4. Flexibility after launch
The phasing loop plan is also very robust in the face of missed maneuvers. A missed PM1, for example, can easily be accommodated by modified PM2 and PM3 maneuvers and still get to the Moon at the same time. A missed PM2 is can be accommodated by waiting another month in orbit, and achieving LOI-1 in November. The ability of the plan to easily be modified in the face of contingencies is another strong feature of the phasing orbit approach.
In the pictures below, we see what happens with a missed PM1. The spacecraft stays in 6.4 day orbit for a second rev, and then raises to a 11.25 day orbit with a 41 m/sec maneuver. At the final perigee (Pf or PM3) we execute a -8 m/sec maneuver to bring apogee down to Lunar altitude.
The plan is also robust to a missed PM2 maneuver. This profile would require LADEE to wait an extra month in Earth orbit. The gray orbits indicate the first month. We show the trajectory starting after PM1 moving towards PM2. Once PM2 is missed, the spacecraft spends 2 more revs in the grey (moving through the 4th quadrant) and then the approach pattern starts again.
Phasing loops offer several advantages to the mission planner. At the expense of longer operation costs, phasing loops have offer a reduced TCM budget in the face of large launch dispersions, expanded launch windows, and over-all robustness to contingencies.