As I was watching the great success of the New Horizons team, I became motivated to do a bit of quick “back of the envelope” calculations to re-create the trajectory. I don’t have to start completely from scratch, because in 2004 I created an STK/Astrogator tutorial giving the basic ideas of how to set up the New Horizons trajectory:
Astrogator New Horizons Tutorial
I thought it would be fun to update things and make them closer to what was actually flown. I can easily do so because the New Horizons Astrogator Yanping Guo (along with legendary Astrogator Bob Farquhar) gave me what I need in this paper:
Yanping Guo and Bob Farquhar: New Horizons Mission Design
I will refer to this from now on as “Yanping’s paper” just for simplicity, but Farquhar helped write it as well.
I’m going to do this in STK/Astrogator, but the basic idea would be similar in other software. I’ll update my scenario a bit to include the launch portion along with the published B-plane parameters at from Yanping and see if our geometry lines up with hers. (STK/Astrogator was actually used for the New Horizons mission, which makes this even more relevant. It was also used on Messenger, LRO, LCROSS, LADEE, etc… but I digress.)
Launch Targeting
Firstly, let’s get the launch set up, so that I can hit the right time of the launch coming out of KSC. The Launch vehicle used was an Atlas 551, a beast of an Atlas with 5 solid boosters, a Centaur upper stage, a Star 48B on top and the 5 meter fairing. That’s actually one heck of a stack of stages. Here’s a really cool report of the launch events, according to Jonathan McDowell:
Jonathan’s Space Report No. 560
“The powerful Atlas 551 rocket, with five solid boosters, roared off the Florida pad after two days of delays. The solids separated at 1 min 45s into launch, arcing into the mesosphere before falling to Earth. The 5-meter-diameter fairing separated at 3min 23s, followed seconds afterwards by the two pieces of the CFLR (Centaur Forward Load Reactor), a contraption that connects the smaller 3.1m-diameter Centaur to the fairing for structural stiffness. By this time Atlas was in space, with the fairing probably reaching an apogee of 150 km or so. Atlas shut down at 4min 27s, falling away 6s later, and the Centaur second stage ignited at 4min 33s as the trajectory flattened out, reaching orbit insertion at 1910:08 UTC with a 167 x 213 km parking orbit. The vehicle coasted for 20 minutes and restarted over South Africa, with a 9-min burn taking the Centaur to 800 km altitude at a velocity of 12.4 km/s, a hyperbolic Earth orbit which will take the Centaur out to the asteroid belt. At 1939 UTC the spin-table on the forward end of the Centaur began to rotate, and the injection stage with the payload separated. The injection stage is an Alliant (Thiokol) Star 48B solid motor, the same motor used on Delta 2 third stages and on the old Shuttle PAM-D flights. Solid kick motors like to be spinning when they fire to even out any misalignment of the thrust direction, hence the spin table – although the Star 48B also has a set of small hydrazine rockets to correct any unwanted nutation. After the Star 48B burn, the payload had reached escape velocity not only with respect to the Earth but also relative to the Sun (The velocity was 16.2 km/s relative to the Earth and I estimate an asymptotic velocity of 12.3 km/s, corresponding to 42.6 km/s relative to the Sun and leading to a heliocentric eccentricity of around 1.05)”
(You should follow Jonathan on twitter: @planet4589 and you can find the latest version of his “Jonathan’s Space Report” here: Jonathan’s Space Report)
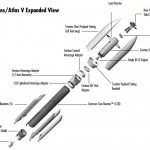
I have to divert a bit from my deep space trajectory because I’m geeking out about the Atlas 551. That’s a sweet rocket. Let’s see a picture of the stack from the launch press kit:
Ok, let’s just look at rocket itself. (You really want to click on this one, it’s a cool rocket!)
The Star 48B is a very reliable (and available) upper stage, and stacking it on top of a Centaur is pretty unusual, but necessary for the high C3 (157.64 km^2/sec^2). That C3 is (as noted by Jonathan) hyperbolic with respect to the Sun!
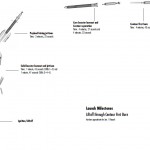
Let’s take a quick look at the staging profile (also from the press kit):
Our purpose here is to duplicate the interplanetary trajectory, so I’m not compelled to completely duplicate the launch segment. I’m going to model all burns as impulsive burns (I don’t have their engine models anyway) and I’m going to combine the Centaur and Star 48B into one insertion burn. It’s fine to do this, since ultimately the multiple insertion burns are just targeting a single trajectory after launch, with a single defined asymptote. The Centaur and Star48 burns were optimized to hit a single asymptote, so I’ll just model that part.
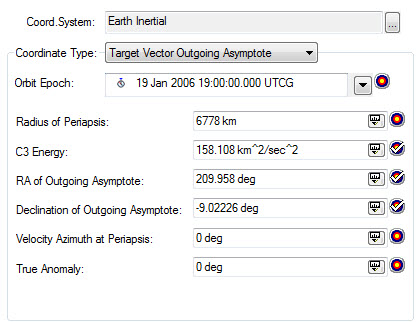
From my NH tutorial mentioned earlier, I will re-use these asymptote conditions:
These conditions came originally from Trajopt (an old DOS program written at SAIC) and they’ll be good enough. I could have gotten them from a variety of other sources that help you search for planetary swingby opportunities. I’ve used MAnE, Trajopt and “Swingby Calculator”, and there are many others. Regardless, these conditions are plenty good and they ought to get me to the Jupiter swingby, and then I’ll work from there.
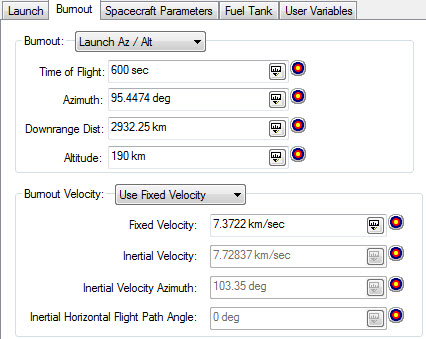
So I will launch out of KSC with these conditions:
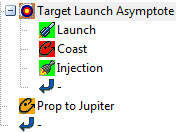
In STK/Astrogator, we model the launch as a portion of an ellipse that starts at the ground and then meets the launch insertion state. This is a decent estimate of the burnout state. After the launch, we’ll coast in orbit for a bit, and then execute an escape maneuver. The mission control sequence for that looks like this:
So I’ll vary my launch time (to get the orbital plane, or the Right Ascension of the asymptote) , my coast duration before the impulsive escape delta-v (to get the Declination of the asymptote) and the delta-v itself (to get the C3, or energy) to hit the asymptote conditions. When I do that, I get this type of a flyby at Jupiter:
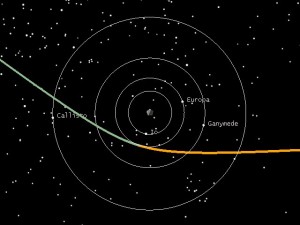
So using the Trajopt asymptote does actually create an encounter with Jupiter, but I don’t get anywhere near Pluto. According to Yanping’s paper, my flyby should look like this:
But if you go into the Jovian system for my flyby, you’ll see this:
So that tells me that the asymptote isn’t going where I want. I can fix that pretty easily. Yanping gives me the B-plane parameters I need at Jupiter to continue on the Pluto. If I match these parameters, I should then be close enough to an encounter with Pluto that Astrogator can target me the rest of the way in. I’ll match them by slightly varying my departure asymptote parameters.
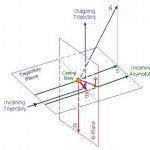
The B-plane is a fictional plane that is used for precise targeting during a gravity assist or for planetary orbit insertion. It can be best thought of as a bulls-eye or target plane attached to the assisting body. The trajectory’s intersection point on the B-plane is where the spacecraft would go if the swingby planet had no gravity. This turns out to be useful because B-plane targets behave very linearly as you move the trajectory around (while targeting) while the actual periapsis point (or closest approach point) doesn’t move very linearly near the planet due to the non-linear force of gravity.
The B-plane is defined to be the plane that contains the focus (usually the center of mass of the body) of an idealized two-body trajectory (assumed to be a hyperbola) that is perpendicular to the incoming asymptote of that hyperbola. The incoming and outgoing asymptotes, S and O, and the focus of the hyperbola are contained in the trajectory plane, which is perpendicular to the B-plane. The intersection of the B-plane and the trajectory plane defines a line in space. The B-vector is defined to lie along this line, starting on the focus and ending at the spot where the incoming asymptote pierces the B-plane. A reference vector (R) is used to externally define the other planar axis. There are different choices to use for R. Typical examples are the planet’s orbit normal, or the planetary pole vector. You can use whatever you want, as long as you specify what it is (so others can duplicate what you’re doing, like I’m about to do)
The vectors T and R lie in the B-Plane and are used as axes. The coordinates of our point in the coordinate system defined by those axes are called BdotT and BdotR, and they are the standard parameters given that allow you to target a swingby.
My initial state from Trajopt gives me the right direction for my transfer trajectory to get close to our B-plane targets (i.e. somewhere in the Jovian system), but I’m going to substitute in the B-plane parameters from Yanping’s paper instead of those that Trajopt originally generated. This should get me close enough to Pluto to hit our B-plane targets later.
I will target the following at Jupiter (From Yanping):
B-Plane Target:
B dot T = 342421 km
B dot R = 2629560 km
Jupiter Periapsis (closest approach) time = 28 Feb 2007 12:00:00.000 UTC
(Jupiter’s North Pole Reference frame)
I’ll use these parameters for now, and then let them be varied later. On the real mission, Yanping used trajectory correction maneuvers (planned for up to 25!), and didn’t try to accurately hit the Pluto B-plane precisely all the way back from launch. I can get away with that here, so I will. If I wanted to simulate how a real mission would do it, I’d truncate off my asymptote solution back at Earth, and our B-plane targets at Jupiter and recover from those errors with TCMs. In a numerical simulation, I can pretend that I can hit targets much more precisely than I can in real life, so I’m going to cheat here and do that.
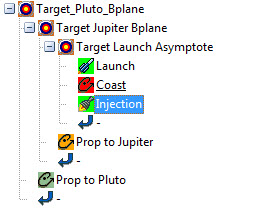
I will use a double-nested targeter to achieve our goals. The inner targeter varies the Launch Time, the Coast duration, and the Injection delta-v to achieve the asymptote conditions. The outer targeter will vary the asymptote conditions of the inner targeter (RA, Dec and C3 of outgoing asymptote), in order to achieve the desired B-plane parameters and arrival epoch at Jupiter. So I’m going to let the targeter vary my first guess at the outgoing asymptote from Earth (the guess that came from Trajopt) in order to hit the B-plane parameters that Yanping says I need. The Astrogator MCS for this is below:
After this converges, my trajectory looks like this (view at Pluto closest approach):
Which is a lot closer. The Pluto arrival date isn’t exactly right and while it looks close on the solar system scale, I am actually 5.9 million km from Pluto at periapsis. This shouldn’t surprise me though, because I haven’t really targeted anything at Pluto yet. I am relying solely on the Jupiter B-plane parameters to get us there. At the Jupiter flyby, my geometry looks like this:
Which looks a lot more like the encounter geometry that Yanping showed in her paper. So now, I’d like to actually target my Pluto periapsis to the right spot and at the right time to match the encounter.
Again, I’ll rely on Yanping’s paper to tell me what I want to hit:
B-Plane Targets:
B dot T = -10910.6 km
B dot R = 2041.9 km
Pluto Periapsis (closest approach) time = 14 Jul 2015 11:58:59 UTC
(Pluto orbit normal frame)
I will target this with a triple nested targeter (highly bogus in terms of trajectory realness in this case, but cool anyway). It looks like this:
1. The deepest internal targeter (Target Launch Asymptote) varies the launch time, coast duration, and burn delta-v to hit the outgoing asymptote (RA, Dec and C3 of asymptote)
2. The second targeter (Target Jupiter Bplane) varies the outgoing asymptote conditions of the deepest targeter in order to hit B-plane parameters at the Jupiter swingby.
3. The outermost targeter (Target Pluto Bplane) varies the B-plane parameters at the Jupiter Swingby in order to hit the desired B-plane parameters at Pluto.
This setup is simple but powerful and gets an answer, but I couldn’t really do this when flying a mission. It essentially has me targeting the Pluto B-plane accurately from conditions all the way back at insertion in Earth orbit! Launch vehicles can’t hit the asymptote RA and Dec within 0.000001 degrees, nor can injection maneuvers be executed with precision of 10e-6 meters. I’m going to ignore that though, since I know I’d have to do midcourses, and just enjoy the coolness of the trajectory.
So in my uber-precise mathematical universe we get this at arrival:
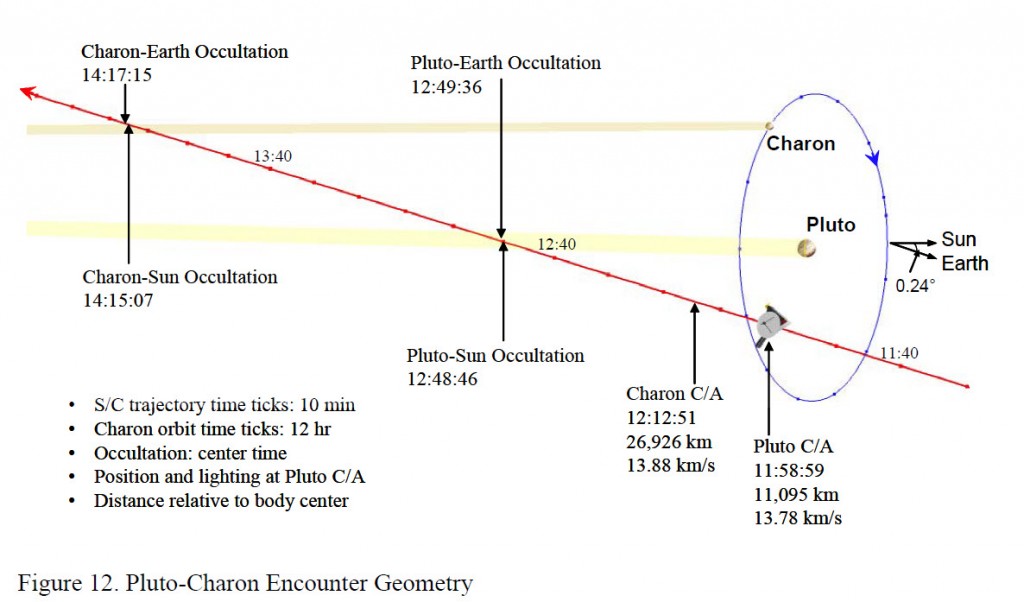
From Yanping’s paper she has the geometry looking like this:
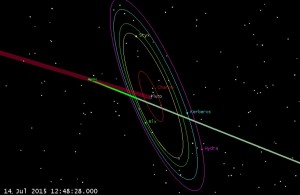
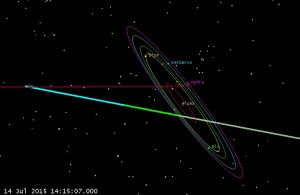
We can also look at both sun occultations to see if they match up:
And they do (which is pretty satisfying!) Of course our fellow Astrogator Yanping Guo had to do things much differently than this, since she had to correct out insertion errors, attitude dumps, and Orbit Determination (OD) errors, etc. all along the trajectory for 9.5 years! In fact while they had planned 25 Trajectory Correction Maneuvers (TCMs), they only had to perform 9, which saved them 2/3 of the planned delta-v. This gives them plenty of delta-v to use to retarget to a Kuiper belt object later this year (pending additional NASA funding). Once they announce the target KBO object, I’ll update and extend my trajectory to match.
Also, I think the final conditions at the encounter may have been slightly off from what I have here (due to TCMs, adjustments, etc. that occurred after the paper was written). Once I get my hands on those conditions, I can trivially re-target things to achieve those states instead of what I hit above. (and I will, and will update here). What I’ve found so far has been conflicting, so I’ll stick with the paper. If someone has better data, pass it on. It’s easy to re-do.
I end this fun with a bit of animation showing the Plutonian system in action. I’d been wanting to see an animation of the system with the dual-planets co-orbiting, so I just made one myself. I love seeing Pluto dancing around the system barycenter. Planet and moon positions come from JPL SPICE files.
Here’s a link to the STK scenario.
If you’d like an ephemeris in a non-STK format, email me and I’ll create one for you.

![New Horizons Atlas 551 (5 meter fairing, 5 solids, 1 RL10 on the Centaur) [Click to enlarge]](https://astrogatorsguild.com/wp-content/uploads/2015/07/NewHorizons_Rocket_Bly-225x300.jpg)

![New Horizons Jupiter Flyby (from Yanping's paper sited earlier) [Click to Enlarge]](https://astrogatorsguild.com/wp-content/uploads/2015/07/yanping-flyby-geometry-300x221.jpg)


![New Horizons Trajectory with Jupiter Bplane Targeting [Click to Enlarge]](https://astrogatorsguild.com/wp-content/uploads/2015/07/bplane_target2-300x169.jpg)